Criterios de semejanza de triángulos

1Dos triángulos son semejantes si tienen dos ángulos iguales.

2 Dos triángulos son semejantes si tienen los lados proporcionales.

3 Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.

                                                                           publicado por : wendy canales

Teorema para el reportee # 3

Teorema:
Los triángulos BED y CED tienen la misma área, porque tienen la misma base y la misma altura.
Ejemplo:
Calculemos el área del triángulo ADE: Será AD . h / 2 = AE . h' / 2
Calculemos el área del triángulo CDE: Será CD . h / 2
Calculemos el área del triángulo BED: Será BE . h' / 2
Como las áreas de los triángulos BED y CDE son iguales, los cocientes ADE / BED y ADE /CDE serán iguales.
Entónces AD / CD  = AE / BE 







Publicado por: Solange Felipa

Juego matematicoo

 Aquii un jueguitooo paraa los qee estan estresedaaaados cn lo de los reportees, se estreseen MAS :)





El cuadrado que ves en la imagen ha sido divido en 4 cuadrantes de igual tamaño,

a los que llamamos, A, B, C y D de acuerdo con lo ilustrado en la figura.
A continuación se te van a plantear 4 desafíos para que los resuelvas.

Desafio 1:
Mentalmente, divide el área blanca del cuadrante A, de modo que resulten 2 piezas de igual tamaño.
asi:

 Desafio 2:
Mentalmente, divide el área blanca del cuadrante B, de modo que resulten 3 piezas de igual tamaño.

Desafio 3:
Mentalmente, divide el área blanca del cuadrante C, de modo que resulten 4 piezas de igual tamaño.



Desafio 4:
Mentalmente, divide el área blanca del cuadrante D, de modo que resulten 5 piezas de igual tamaño.

Lo hicistee?

Miraa las solucioness:

1.

2.

 3.

 4.

Les gustoo? a mi no :) haha no mentiraaa

Publicado por: Solange Felipa

Como hacer los "amados" reportees :)

Para los qe estaaan perdidos (como yo¬¬) en hacer los reportees aaqui estan los pasos qe yaltaa nos dijo:

1. Antecedentes
2. Aspectos teoricos
3. Experiencia
4. Resultados
5. Conclusiones y recomendaciones

ESOS SON :)




Publicado por Solande felipa

Principio de Arquímedes

Principio de Arquímedes

El principio de Arquímedes afirma que todo cuerpo sumergido en un fluido experimenta un empuje vertical y hacia arriba igual al peso de fluido desalojado.
La explicación del principio de Arquímedes consta de dos partes como se indica en la figuras:

1. El estudio de las fuerzas sobre una porción de fluido en equilibrio con el resto del fluido.
2. La sustitución de dicha porción de fluido por un cuerpo sólido de la misma forma y dimensiones.

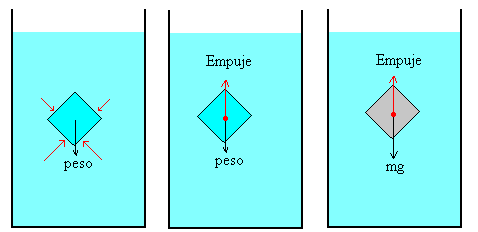Porción de fluido en equilibrio con el resto del fluido.
Consideremos, en primer lugar, las fuerzas sobre una porción de fluido en equilibrio con el resto de fluido. La fuerza que ejerce la presión del fluido sobre la superficie de separación es igual a p·dS, donde p solamente depende de la profundidad y dS es un elemento de superficie.
Puesto que la porción de fluido se encuentra en equilibrio, la resultante de las fuerzas debidas a la presión se debe anular con el peso de dicha porción de fluido. A esta resultante la denominamos empuje y su punto de aplicación es el centro de masa de la porción de fluido, denominado centro de empuje.
De este modo, para una porción de fluido en equilibrio con el resto, se cumple
Empuje=peso=r_f·gVEl peso de la porción de fluido es igual al producto de la densidad del fluido r_f  por la aceleración de la gravedad g y por el volumen de dicha porción V.
Se sustituye la porción de fluido por un cuerpo sólido de la misma forma y dimensiones.
Si sustituimos la porción de fluido por un cuerpo sólido de la misma forma y dimensiones. Las fuerzas debidas a la presión no cambian, por tanto, su resultante que hemos denominado empuje es la misma y actúa en el mismo punto, denominado centro de empuje.
Lo que cambia es el peso del cuerpo sólido y su punto de aplicación que es el centro de masa, que puede o no coincidir con el centro de empuje.


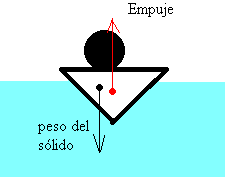
- Por tanto, sobre el cuerpo actúan dos fuerzas: el empuje y el peso del cuerpo, que no tienen en principio el mismo valor ni están aplicadas en el mismo punto.
En los casos más simples, supondremos que el sólido y el fluido son homogéneos y por tanto, coinciden el centro de masa del cuerpo con el centro de empuje.
          publicado por wendy canales

biografia de arquimedes

Biografia de arquimedes
precursor en la fisica , matematico y fisico en la antigua grecia Estableció el llamado Principio de Arquímedes

Defendió Siracusa, su ciudad natal, con aparatos de su invención como las catapultas y los espejos cóncavos, con los que incendiaba naves cuando los romanos la sitiaron. Inventó la palanca, el tornillo sin fin y las ruedas dentadas. Fue el creador de la mecánica estática y determinó el empuje que Imprime un fluido un sólido (principio de Arquímedes). Enseñó el cálculo de raíces cuadradas, determinó perímetros con toda exactitud, calculó valores aproximados a r, resolvió ecuaciones cubica  ecuaciones cúbicas con la ayuda de secciones cónicas. En el campo de la física descubrió las leyes del centro de la gravedad y del plano inclinado. Se le adjudica una instalación mecánica de riego y aparejos. Cuando por fin Siracusa fue tomada, un soldadoromano lo mató por error. Se conservan nueve de sus escritos: De la esfera y del cilindro, Sobre la medida del círculo, Conoides y esferoides, Sobre las hélices; Equilibrio de los planos, Sobre la cuadatura de la parábola, El arenario, Equilibrio de los cuerpos flotantes y metodo respectoa los teoremas mecanicos ..

                                                                          publicado por :wendy canales

                   Razones trigonométricas

 

Razones trigonométricas en un triángulo rectángulo

                Signo de las razones trigonométricas

                                                         

  

Tabla de razones trigonométricas

Relaciones entre las razones trigonométricas

• cos² α + sen² α = 1
• sec² α = 1 + tg² α
• cosec² α = 1 + cotg² α

                                                               PUBLICADO : MAROLY GORDILLO